Holiday reading

It's a sunny Memorial Day afternoon in Butte, and I'm kicked back with my knee on ice, reading Volume I of the 4-volume series The World of Mathematics. We usually take the dogs for a hike on Memorial Day, but that's not an option this year so we're having a relaxing day at home instead.
I decided to take a break from reading to write up some thoughts on this series of books, which I've been fascinated by since I was in grade school.
Trigger Warning: if you find math boring or annoying, now would be a good time to stop reading.









A few photos from past Memorial Day holidays.
Recovery time is reading time
Having scheduled my knee surgery well in advance (I made the appointment seven months ahead of time), I had plenty of time to plan various details. And knowing that I'd have lots of reading time while icing my knee during the first days and weeks of recovery, I decided to spend that time finishing a work that I started several times long ago but had never finished: James R. Newman's 4-volume, 2500-page collection of essays on mathematical topics, The World of Mathematics.
"Started" is probably overstating things. My Dad had a copy, and I flipped it open a few times to read things that I found interesting as a kid, but I never actually started on Page 1 and tried to read it all the way through. Being a young math geek, the things I found interesting back then were mostly stories of child prodigies, such as those covered in W. W. Rouse Ball's entertaining essay on "Calculating Prodigies."
One story I remember vividly was the famous schoolroom anecdote of Carl Friedrich Gauss, who went on to be considered by many the greatest mathematician of all time:
For his elementary education Gauss was enrolled in a squalid school run by a man named Büttner whose main teaching technique was thrashing. Büttner was in the habit of assigning long addition problems which, unknown to his students, were arithmetic progressions that he could sum up using formulas. On the first day that Gauss entered the arithmetic class, the students were asked to sum the numbers from 1 to 100. But no sooner had Büttner stated the problem than Gauss turned over his slate and exclaimed in his peasant dialect, "Ligget se'." (Here it lies.) For nearly an hour Büttner glared at Gauss, who sat with folded hands while his classmates toiled away. When Büttner examined the slates at the end of the period, Gauss's slate contained a single number, 5050—the only correct solution in the class.
Having enjoyed a few simple stories like that from The World of Mathematics long ago, I decided to use my knee surgery recovery time as an opportunity to fill in the gaps and read the entire series.
What it is
The World of Mathematics is a collection of essays on mathematical topics. Most of the essays were written by historically notable mathematicians and first published in other places, although some were written by Newman himself to cover mathematical developments that he felt hadn't been well documented by others. His goal was to create an anthology covering the aspects of mathematical thought that he found most interesting or enjoyable, and make it accessible to the layman in a way that would "convey something of the diversity, the utility, and the beauty of mathematics."
Newman did not set out to create a complete or authoritative history of mathematics, and the essays he selected are his own opinionated collection. As he notes in the introduction,
"An anthology is a work of prejudice. This is no less true when the subject is mathematics than when it is poetry or fiction. Magic squares, for example, bore me, but I never tire of the theory of probability. I prefer geometry to algebra, physics to chemistry, logic to economics, the mathematics of infinity to the theory of numbers. I have shunned topics, skipped some, and shown great hospitality to others. I make no apology for these prejudices; since I pretend to no mathematical skill, I have felt at liberty to present the mathematics I like."
There are 133 essays in the collection, ranging from a few pages to several longer pieces that had previously been published as books in their own right. Some cover a key development or noteworthy person in mathematical history, but there are also essays that are pure entertainment. Here are a dozen examples of the wide range of topics covered:
- "The Sand Reckoner" by Archimedes
- "The Ability of Birds to 'Count'" by O. Koehler
- "The Seven Bridges of Königsberg" by Leonhard Euler
- "Mathematics of Motion" by Galileo Galilei
- "John Couch Adams and the Discovery of Neptune" by Sir Harold Spencer Jones
- "Heredity and the Quantum Theory" by Erwin Schrödinger
- "Statistics of Deadly Quarrels" by Lewis Fry Richardson
- "Mathematics of a Lady Tasting Tea" by Sir Ronald A. Fisher
- "Symbolic Notation, Haddocks' Eyes and the Dog-Walking Ordinance" by Ernest Nagel
- "How to Hunt a Submarine" by Philip W. Morse and George E. Kimball
- "Cycloid Pudding" by Jonathan Swift
- "Common Sense and the Universe" by Stephen Leacock
Newman may not have set out to document the history of mathematics, but that's essentially what he accomplished: his collection of essays is so extensive and diverse that it's a pretty thorough historical overview. There are essays covering the early innovations of the ancient Babylonians, Egyptians, and Greeks, the contributions of Indian mathematicians (e.g., the decimal system), the role of Arabic scholars in preserving the canon of ancient mathematical knowledge through the Dark Ages, the explosion of mathematical innovation across Europe starting in the 16th Century, and 20th Century essays by Kurt Gödel, Alan Turing, Albert Einstein, and others.
About the author
In revisiting this work, I realized that I knew nothing about the man who had put it together. So I did some research and learned a few things about the life of James R. Newman, which was more interesting and varied than I would have guessed.
Born in New York City in 1907, Newman breezed through law school at Columbia and was a practicing lawyer in New York from 1929 to 1941. During this time, he was also a keen student of mathematics.

In 1940, while still practicing law, Newman co-authored a book entitled Mathematics and the Imagination, a concise summary of modern mathematics which quickly became a best-seller. Reviewers praised its "graceful style, combining clarity of exposition with good humor," and noted that it "succeeded in communicating to the layman something of the pleasure experienced by the creative mathematician in difficult problem solving."
Mathematics and the Imagination is most famous for introducing a new piece of mathematical jargon: googol, the name for the huge number 10^100 (a 1 followed by one hundred 0s). This term was used in a chapter entitled "Beyond Googol" that explained the critical differences between infinite and very large but finite numbers. Half a century later, two computer science students at Stanford University decided to name their new search engine after the term googol, but accidentally misspelled it. When they realized they had registered their domain as google.com, they decided to stick with the misspelled version, and named their company Google. (I think twelve year old me would have found it pretty cool that I would someday work for a company named after googol.)
After publication of Mathematics and the Imagination, Newman decided in 1941 to start work on his vision for The World of Mathematics, which he hoped to finish in a couple of years. But work on this new project was delayed when Newman found himself pulled into the events surrounding World War II.
After Pearl Harbor led to the United States' entry into the war, Newman was appointed Chief Intelligence Officer at the US Embassy in London, a role he retained through the end of the war. After that, he was a member of the team that drafted the Atomic Energy Act of 1946, and also contributed to an influential 1948 book entitled The Control of Atomic Energy, which outlined the social, economic, and political implications of this new technology.
While Newman was distracted by world events, the success of Mathematics and the Imagination opened some doors for him, most notably leading to the award of a fellowship from the Guggenheim Foundation in 1946. That fellowship gave him the financial freedom to devote most of his time to The World of Mathematics, and in 1956 it was finally finished and published by Simon & Schuster, 14 years in the making.
A couple of years later, my father — a PhD student in chemical engineering at Montana State University at the time — purchased a copy of The World of Mathematics. The binding on that copy was falling apart a few years ago, so I replaced it with a barely used copy that I found on eBay, which is the copy I'm reading today.
Stories > equations
“No, no! The adventures first, explanations take such a dreadful time.”
― Lewis Carroll, Alice’s Adventures in Wonderland / Through the Looking-Glass
Some may wonder how a book of mathematical equations could hold one's interest for 2500 pages. And the simple truth is that, unless you're wired like Paul Erdős, the eccentric Hungarian mathematician who lived for math and absolutely nothing else, it probably can't. (Erdős famously said "a mathematician is a machine for turning coffee into theorems," which pretty much sums up how he spent his entire life.)
In reading The World of Mathematics, I often find myself getting bored with the math itself and skimming the equations. Twelve year old me would probably be disappointed in that confession, but at this point in life the parts I find most fascinating are the stories of the people involved. Mathematicians throughout history and across cultures have constantly built upon each other's work, and the collision between so many strong personalities, massive egos, and brilliant minds has led to inevitable drama and conflicts.
For example, it is widely known that both Sir Isaac Newton (a proud Englishman) and Gottfried Wilhelm Leibniz (a proud German) independently developed the concept of calculus, the mathematical study of continuous change. Newton developed it first, but Leibniz came up with a cleverly compact notation that was easier to work with than Newton's, in which he used the symbol ∫, or a "long S" to signify a series of sums, and d for the differential rate of change. Newton had given England a head start in calculus, but their lead was squandered by a stubborn insistence on clinging to Newton's inferior and inefficient "English" notation, while the great mathematicians across Europe – Bernoulli, Euler, and Fourier, for example – embraced Leibniz's straightforward "German" notation and took calculus to new heights. Leibniz's notation is now taught in every calculus curriculum in the world, and Newton's notation is a historical footnote.
You don't need to understand the underlying math to enjoy a story like that any more than you need to understand the underlying molecular chemistry to enjoy the story of Walter White developing a new approach for manufacturing crystal meth in "Breaking Bad." And The World of Mathematics is full of those sorts of stories.
One aspect of the Newton-Leibniz story is a recurring theme through mathematical history: the concept of an improvement in notation being the key development that enables other mathematical breakthroughs. For example, The Whetstone of Witte written by Welsh physician Robert Recorde in 1557 was the first time an English writer used the plus and minus signs, and also was the first recorded use of the equals sign. These notational improvements enabled Descartes, Newton and others to accelerate the pace of mathematical innovation in the decades that followed Recorde's work. When you peel back the layers of the onion of mathematical history, it's notational improvements all the way down.
But I'm getting ahead of myself, talking about the details of this great series while I'm still plodding through Volume 1. I'll probably do a more thorough blog post about The World of Mathematics when I'm done, but first I have a bunch of reading to do!
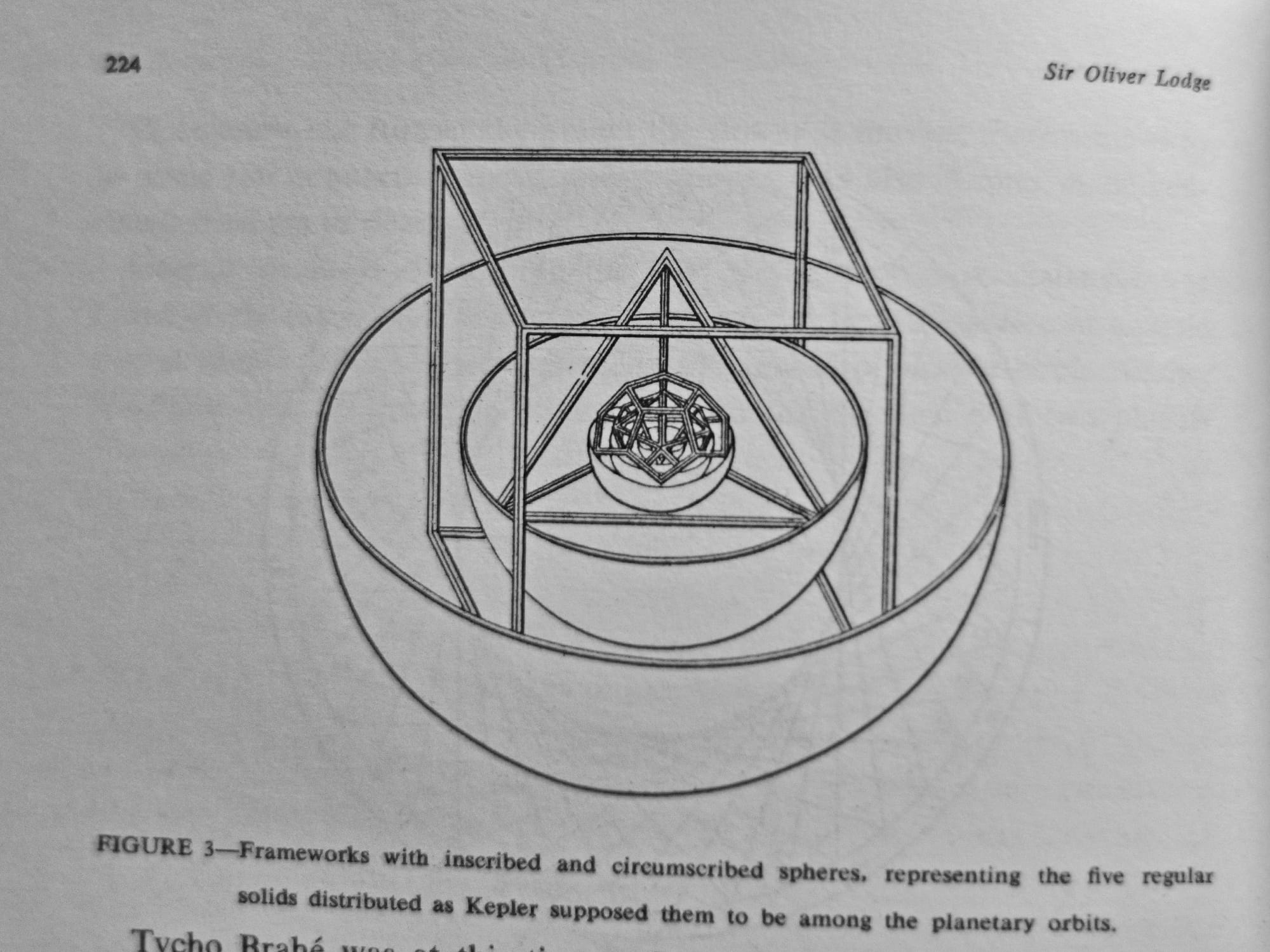
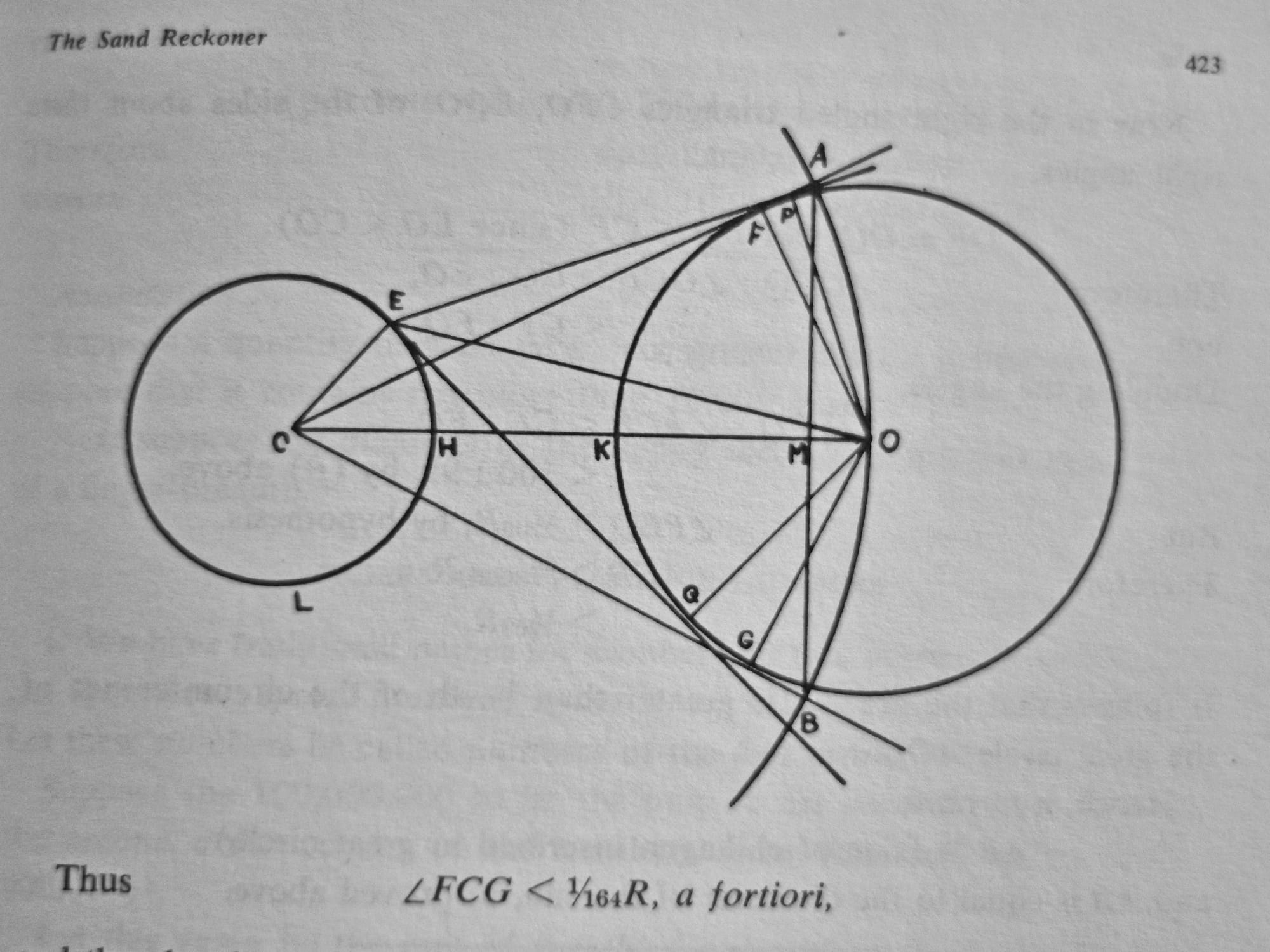

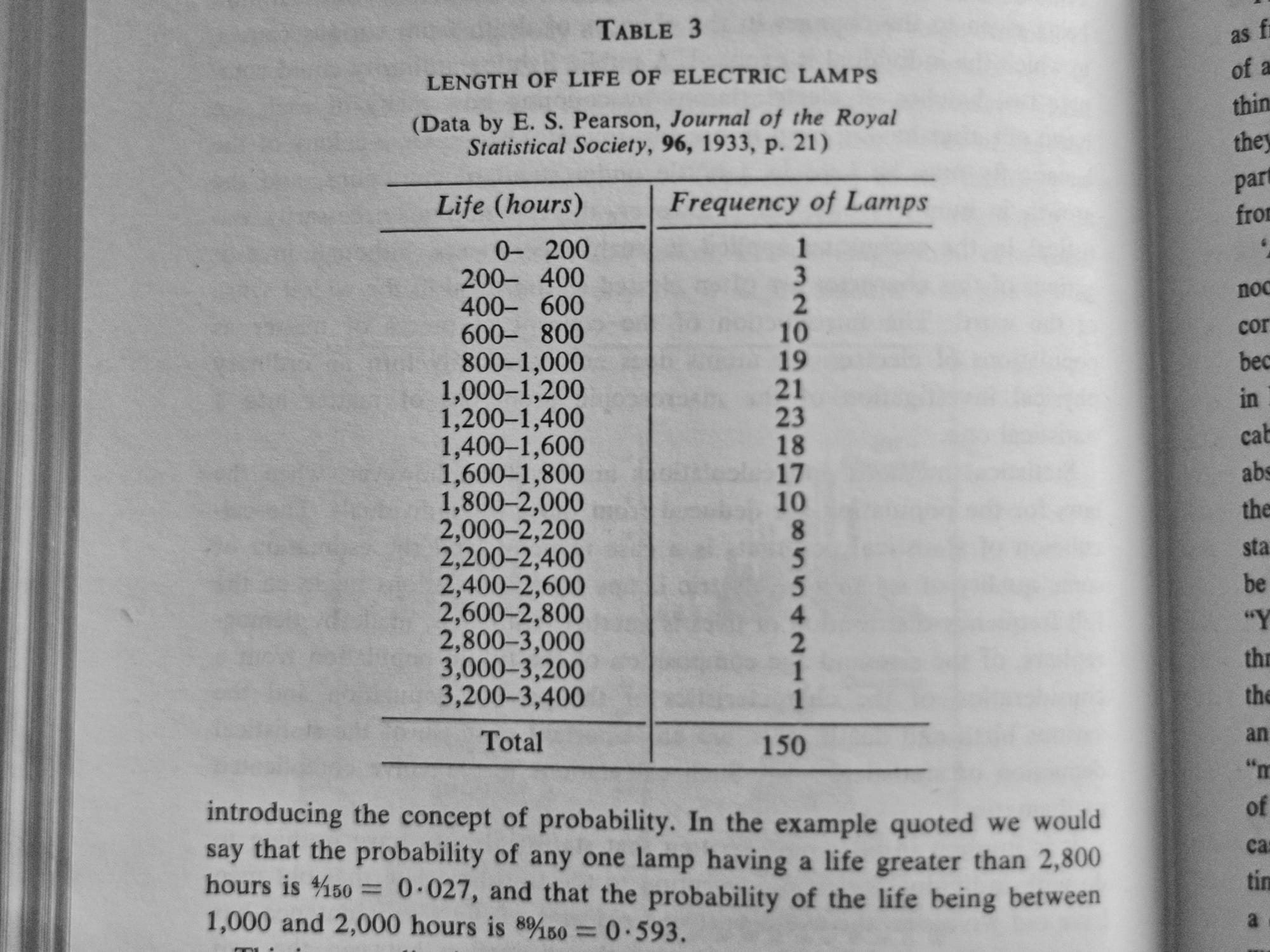
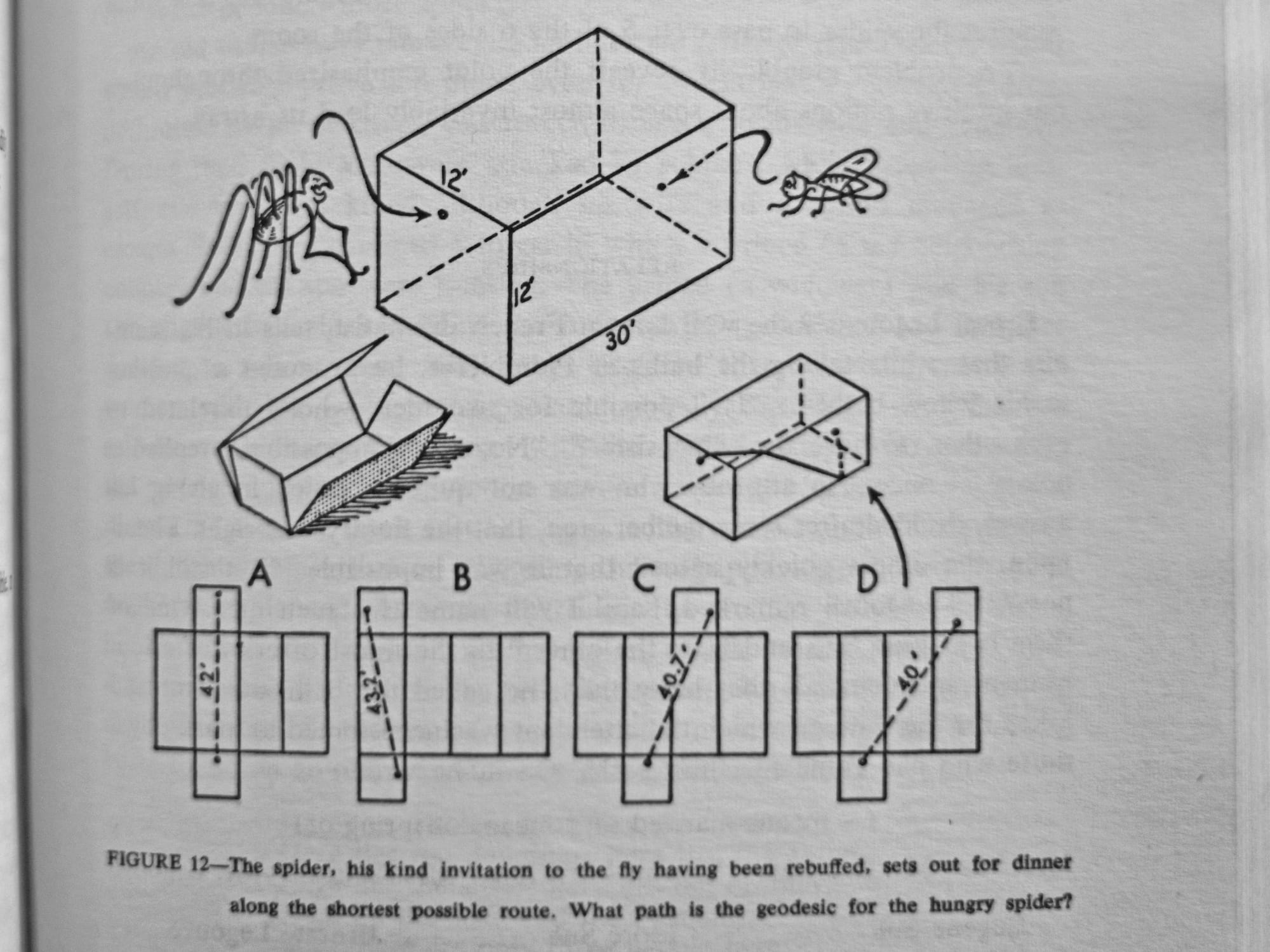
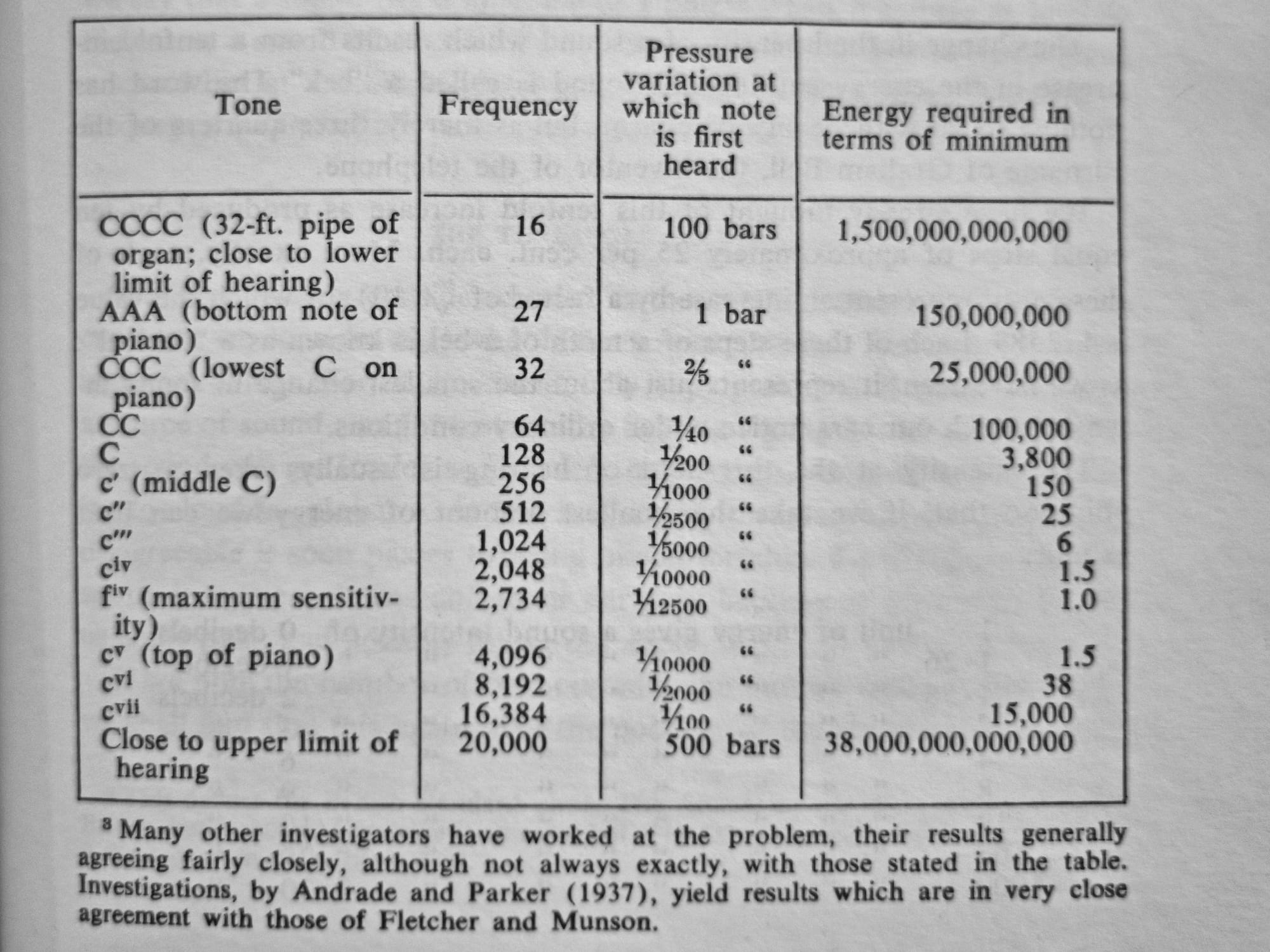
A few examples of the many illustrations and tables in The World of Mathematics.
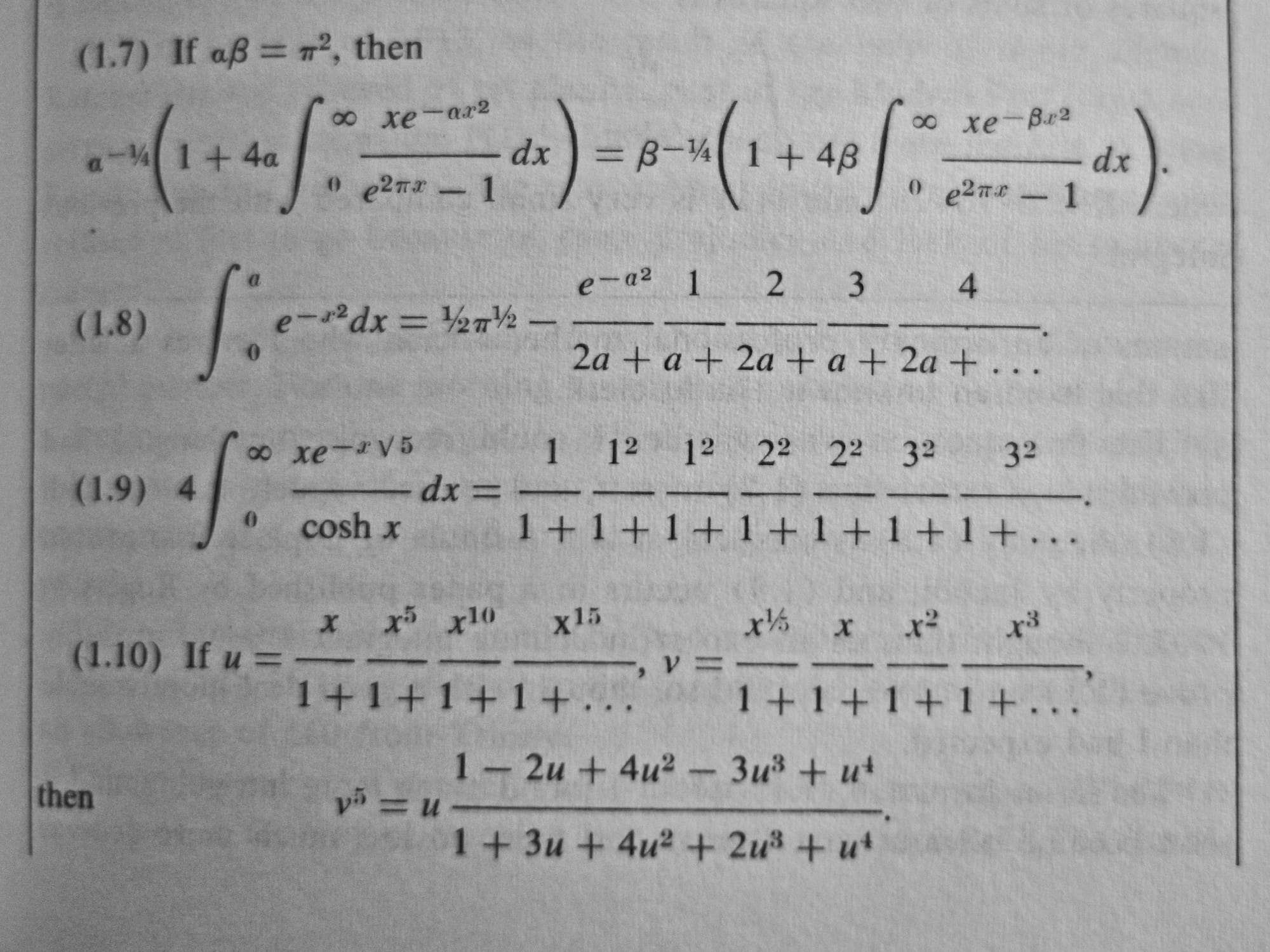



I brought Volume I along for the trip to Seattle for my knee surgery, but in hindsight it was naive to think I'd read much of it in that first week. This is not a book you can enjoy with opioid painkillers coursing through your veins and dulling your senses. :) So I set it aside for a while, but now on Day 13 of my recovery, taking nothing but Tylenol, I'm diving back in.