Fun With Math
This post is something I wrote in 1996 for my niece Madeline, who was 9 years old at the time. It was an attempt to convey to her some of the things I found interesting about numbers and arithmetic when I was her age.
BIG Numbers
There are big numbers, and then there are BIG numbers. Here are some big numbers …
- 200,000 the number of people in Spokane
- 3,000,000 the number of people in Chicago
- 4,000,000,000 the number of people in the entire world
Sometimes it’s hard to tell the difference between big numbers. Especially when they have all of those 0’s in them. Who could notice the difference between 10,000,000 and 100,000,000, without looking closely?
Luckily, all of these numbers have names to help us keep track of them. The number of people in Spokane, for example, is “two hundred thousand.” The number of people in Chicago is “three million,” and the number of people in the world is “six billion.”
Those numbers aren’t exact, of course. The number of people in the world is really something like 6,525,170,264, or “six billion, five hundred twenty-five million, one hundred seventy thousand, two hundred sixty-four.” But there’s no way to know the exact number.
Why can’t we know the exact number of people in the world? Because it’s always changing – even if you knew the exact number, it would be wrong before you could finish saying it. Scientists tell us that about 3 babies are born every second around the world. So by the time you finish saying “six billion, five hundred twenty-five million, one hundred seventy thousand, two hundred sixty-four,” the real total would be more, but by the time you finish saying the other number there would be more than that, and you could never catch up. So we just round it off and say “six billion.”
Those are pretty big numbers, but we’re not even warmed up yet. Scientists work with much bigger numbers than that. For example:
100,000,000,000,000,000,000 = a scientist’s estimate of the number of grains of sand on the beaches of Coney Island.
How do we say this number? There are two ways to say it.
The first way is to use the same technique we use for numbers like “ten thousand” or “ten million.” With this technique, we group long numbers into groups of 3, and each group has a name. It works like this …
- 1,000 = a thousand
- 1,000,000 = a million
- 1,000,000,000 = a billion
- 1,000,000,000,000 = a trillion
- 1,000,000,000,000,000 = a quadrillion
- 1,000,000,000,000,000,000 = a quintillion
- 1,000,000,000,000,000,000,000 = a sextillion
- 1,000,000,000,000,000,000,000,000 = a septillion
See how each time we add three digits it gets a new name?
So, with this approach, we would say “there are approximately one hundred quintillion grains of sand on Coney Island.”
That’s simpler than saying all of the 0’s, but it’s still pretty hard. You have to memorize those words that end in “illion,” and most people never learn them beyond trillions. Also, some countries define the words differently. For example, in America we say that a billion is a 1 followed by 9 zeroes (a thousand millions), but in Britian they say that a billion is a 1 followed by 12 zeroes (a million millions). This makes it confusing. Luckily, the other way of saying big numbers simplifies things.
The other way to say big numbers is to use “scientific notation.” We call it that because it’s the way scientists talk about big numbers. Here’s what they do … instead of having silly names like “septillion” for big numbers, they just count how long the number is. And if the number is a 1 followed by all 0’s, they say that number is a “power of ten.”
For example, the number 1000 – which you and I would call “one thousand” – is called “10 to the 3rd power” in scientific notation. And the number of grains of sand on Coney Island is a 1 followed by 20 0’s, so in scientific notation that’s “10 to the 20th power.” When you write these numbers down, you put the 10 down below and the power above it, like this: 1020.
This makes it easier to talk about big numbers, and also makes it easier to write them down. Imagine, for instance, that you needed to describe a number that is a 1 followed by 100 0’s. That’s this number here …
10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
Isn’t it much simpler to simply say “10 to the 100th power” or to write down 10100?
What if the number doesn’t start with a 1? Then what?
Well, in that case the scientists simply describe the number as a multiple of a power of ten. Here are some examples …
- 1,000 = “10 to the 3rd”
- 5,000 = “5 times 10 to the 3rd”
- 6,700 = “6.7 times 10 to the 3rd”
There’s a special big number that has a name all its own, and we already saw it above: 10 to the 100th power, or 10100. This special number is called a “googol,” and it was given this name by the son of a mathematician many years ago. Furthermore, a 1 followed by a googol of 0’s is called a googolplex. Now that’s a big number!
You may be wondering, “why do scientists need these big numbers? Is there really anything they have to count so many of?” The answer is no.
Scientists use big numbers like 1020 all of the time, to count molecules or snowflakes or things like that, but they don’t really need numbers like a googolplex – those are just for fun, and for studying numbers alone without applying them to anything in the real world.
Here’s an interesting way to think about what might be the biggest number any scientist would ever need to use: what’s the smallest thing in the world, and how many of them would there be if the whole universe were filled with them? That should tell us the biggest number that a scientist might ever actually need to write down.
The smallest parts of atoms are called protons and electrons – they’re very tiny, and there are more of them in your little finger than the number of grains of sand at Coney Island! But if you filled the entire universe with protons and electrons, scientists estimate that there would be about 10110 of them – more than a googol, but a lot less than a googolplex.
Perfect Numbers
In ancient times, numbers weren’t taken as seriously as we take them now. Some numbers were considered to have mystical powers, and people who studied numbers liked to look for these mystical numbers.
One type of number so fascinated the ancient Greeks that they called them “perfect numbers.” A famous Greek mathematician named Pythagorus, who lived 500 years before Jesus Christ, was among the first to search for perfect numbers.
A perfect number was defined by Pythagorus like this: “a perfect number is equal to the sum of its divisors.” What that means, in plain English, is that you add up all of the numbers that divide evenly into a number, and if they all add up to the number you started with, then it’s “perfect.”
Let’s try it. Is 4 a perfect number?
Well, 4 can be divided by 1 or 2, but not by 3. So the divisors of 4 are just 1 and 2. They add up to 3, which isn’t the same as 4, so 4 is not perfect.
How about 6?
6 can be divided by 1, 2, or 3. And those add up to 6, so 6 is a perfect number!
You can keep looking for them like this, but I’ll save you the trouble …there are only 3 perfect numbers under 1000: 6, 28, and 496. (For 28, the divisors are 1, 2, 4, 7, and 14, which add up to 28.) And after these first few, perfect numbers get rare indeed. The 9th one ever found, for instance, is 37 digits long.
Here’s a type of perfect number that people have tried to find for over 2300 years without success: an odd perfect number. Some mathematicians are convinced that at least one exists, but nobody has been able to find one yet. Whoever finds one – or finds a way to prove that there isn’t one – will be famous in math history.
Power of Two
There are many different types of numbers: odd numbers, even numbers, numbers that end with 0, numbers that start with 1, and so on. One of my favorite types of numbers is “powers of two.”
These are sort of like the “powers of ten” that are used for scientific notation. But with powers of two, instead of adding zeroes for each power, you double the number each time. Here’s how it works …
2 = 21 4 = 22 8 = 23 16 = 24 32 = 25 64 = 26 128 = 27 256 = 28
512 = 29 1,024 = 210 2,048 = 211 4,096 = 212 8,192 = 213 16,384 = 214
32,768 = 215 65,536 = 216 131,072 = 217 262,144 = 218 524,288 = 219
1,048,576 = 220 2,097,152 = 221 4,194,304 = 222 8,388,608 = 223
16,777,216 = 224
See how the number doubles each time? You can continue this pattern as far as you want, and each time you double the number you’ll get a new power of two. When I was in grade school, many nights I counted myself to sleep memorizing these powers of two. I memorized them up to 226, which is 67,108,864.
Years later, when I started working with computers, I found that it’s very handy to know the powers of two. Since computers use powers of two to do their counting, these numbers come up all the time in computer stuff.
For example, you’ve heard people talk about “kilobytes” or “megabytes” when they talk about computers. Well, those are powers of two! A kilobyte is 1024 bytes, and 1024 is 210. And a megabyte is 1,048,576 bytes, which is 220.
Powers of two were taught to students 100 years ago in the United States, but they stopped teaching it because there was no practical use for it. Today, these types of numbers are used in every computer in the world, so schools are starting to teach about them again. You’ll probably see these types of numbers in school some day.
Prime Numbers
Prime numbers are another special type of number. We say that a number is “prime” if it can’t be divided evenly by any other number.
For example, 7 is prime because nothing else divides into it other than 1 or 7.
But 6 isn’t prime, because it can be divided evenly by 2 or 3.
Mathematicians have spent hundreds of years arguing about how to find prime numbers. To this day, nobody has been able to come up with a formula for finding prime numbers. So all of the known prime numbers have been found by actually trying to divide numbers by other numbers: by trial and error. This work keeps some mathematicians very busy, and they’ve now found prime numbers up to dozens of digits long (more than a septillion but less than a googol).
There have been three prime years in the last decade, which is unusual. 1997, 1999, and 2003 are all prime numbers.
1997 also has some other things that make it especially unusual. If you take digits off the front or back of 1997, you always get a prime: 19, 97, 199, and 997 are all prime. The last year where this happened was 1373, and the next time this will happen is 3137. It’s a long ways between years like this!
When you want to figure out whether a number is prime, you have to divide it by smaller numbers. There are some tricks for doing this, which you might find useful some day.
To figure out whether a number is divisible by 2, that’s easy: if it’s even – ending in 0, 2, 4, 6, or 8 – then it’s divisible by 2.
To figure out whether a number is divisible by 3, just add up the digits of the numbers and check whether that’s divisible by 3. You can even add up the digits of the result again and again, until you have a number less than 10. If that number is 0, 3, 6, or 9, then your original number was divisible by 3. Here are some examples …
Is 1987 divisible by 3? Well, 1+9+8+7 is 25, and 2+5 is 7, so the answer is no. 1987 is not divisible by 3, because 7 isn’t divisible by 3.
Is 142,857 divisible by 3? Let’s find out …1+4+2+8+5+7 is 27, and 2+7 is 9, and 9 is divisible by 3, so the answer is yes! We know that 142,857 is divisible by 3, and we figured it out by only doing addition, with no division required.
There are more tricks …
To figure out whether a number is divisible by 4, look at the last two digits. If the 2nd-to-last digit is odd and the last digit is 2, 6, or 0, then it’s divisible by 4. And if the 2nd-to-last digit is even and the last digit is 4 or 8, it’s divisible by 4. From this, we can tell that 65,432 is divisible by 4 but 932,614 is not.
To figure out whether a number is divisible by 5, just check the last digit. If it’s 0 or 5, then the answer is yes. So we know that 12,345,678 isn’t divisible by 5, but 432,765,120 is divisible by 5.
Need to figure out whether a number is divisible by 6? Since 6 is 2x3, all you have to do is check for whether the number is divisible by 2 and also whether it’s divisible by 3 (as described above). If it’s divisible by both 2 and 3, then it’s divisible by 6.
All of those tricks are pretty well-known. But here is one very few people know about: checking for divisibility by 7.
To check for whether a number is divisible by 7, follow this rule: take off the last digit, double it, and subtract that from the rest of the number. Keep doing that until you get down to a number less than 10: if the result is 0 or 7, the original number was divisible by 7, otherwise it wasn’t. Here’s an example of how it works …
Is 945 divisible by 7?
Step 1: Take off the 5, double it to 10, then subtract that from 94.
The answer is 84, which we use to repeat the process.
Step 2: Take off the 4, double it to 8, then subtract that from 8.
The answer is 0, so yes, 945 is divisible by 7.
There are more tricks like this that you can use to test for division by other numbers. By using these little tricks, you can often figure out whether a number is prime without actually doing any messy long division.
Special 7
Seven is a special number in many ways. Here are some fun facts about 7 and its close cousin “one seventh.”
What’s a seventh? Well, it’s 1 divided by 7, which we write down as 1/7. To figure out exactly how much that is, you could take a calculator and punch in a 1, then press the divide key, then press 7, then press the equals key. The answer it would display would look like this: 0.142857.
Depending on the calculator, there might be some more numbers after that. This is because 1/7 is a fraction that turns into a repeating decimal if you write it out. If you had a calculator that was extra-extra-wide, 1/7 would look something like this:
0. 142857142857142857142857142857142857142857142857142857
Here’s a fun thing to do with the number 142,857: add it to itself over and over, and watch how the numbers move around.
For example, 142,857 + 142,857 = 285,714. See how that’s the same numbers but re-arranged? The 1 and the 4 moved over to the back end of the number, but it’s all the same digits.
Let’s add 142,857 to 285,714. The answer is 428,571. It’s the same numbers re-arranged again! The 1 in 142,857 just hopped over to the right side of the other numbers to make 428,571.
If we add 142,857 to this new total of 428,571, we get 571,428. The same numbers re-arranged yet again!
Add 142,857 to 571,428, and you get 714,285. Works again.
After than comes 857,142: all three starting numbers (142) have hopped over the rest (857). Does the pattern ever stop?
Yes it does. Add 142,857 to 857,142 and you get 999,999. And that just happens to be the 7th time we added 142,857 together.
The number 142,857 is related to the number 7 in many ways. For example, if you divide the following fractions on a calculator, here’s what you’ll get …
1/7 = .142857142857142857142857142857142857142857142857142857
2/7 = .285714285714285714285714285714285714285714285714285714
3/7 = .428571428571428571428571428571428571428571428571428571
4/7 = .571428571428571428571428571428571428571428571428571428
5/7 = .714285714285714285714285714285714285714285714285714285
6/7 = .857142857142857142857142857142857142857142857142857142
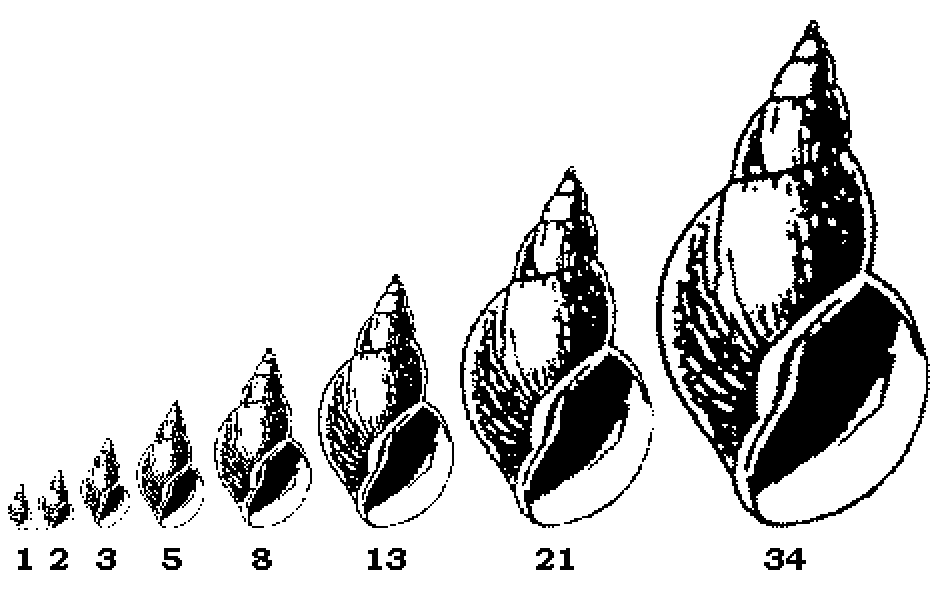
Fibonacci Numbers
As you can see, there are many different types of numbers. For our last look at numbers, I want to show you a type of number that occurs throughout nature. It’s called the Fibonacci series, because that’s the name of the mathematician who first noticed it. His name was Leonardo Fibonacci, and he lived around the year 1250, over 700 years ago. Some of his friends thought he was crazy – they even called him the Italian word for “blockhead” – but he saw a mathematical pattern in nature that nobody else had ever noticed. Fibonacci’s simple pattern shows up in many types of science, including botany (studying plants), biology (studying animals), and astrology (studying stars). It has even been used as an inspiration for artists and architects. Pretty neat for a guy they called blockhead, huh?
The Fibonacci series has a simple rule: add up the previous two numbers, and that’s the next number in the series. So it goes like this …
1
2
3 = 1 + 2
5 = 2 + 3
8 = 3 + 5
13 = 5 + 8
21 = 13 + 8
34 = 21 + 13
… and so on.
There are many places where this series occurs in nature. One of the most common is in the branching of leaves. Some types of plants have leaves that cluster together only in groups of 2, 3, 5, or 8. Flower petals and seeds are also arranged in groups like this sometimes. Look closely at various types of plants, and you’ll find examples of the Fibonacci series.
The Fibonacci series is also related to growth in some types of animals, such as snails. When a snail grows, its shape stays the same even though it’s constantly expanding. The new growth on the outside of a snail’s shell is “added to” the previous growth, and each year’s growth is related to the previous year’s growth in a mathematical series. We could get bogged down in the equations, but you don’t need to see the equations in order to see the pattern. Look at a snail, and look at the stalk of a bushy plant, and try to see how each is growing in the style of the Fibonacci series, adding the most recent numbers together to get the next number each time.
As the numbers in the Fibonacci series grow larger, the ratio between them becomes more and more constant. In other words, you can figure out the next number by multiplying the previous number by a special number (called a ratio), instead of adding them together. That “special number” is between 1 and 2: around 1.6, to be exact.
The ancient Greeks thought this special number was very important, and they called it the golden ratio. They also gave it another name: phi, pronounced “fee.”
If you make a rectangle with the lengths of its sides in the golden ration, that rectangle is called a golden rectangle, and some people believe this is the nicest looking, most “esthetically pleasing” type of rectangle you can make.
Here’s a golden rectangle:


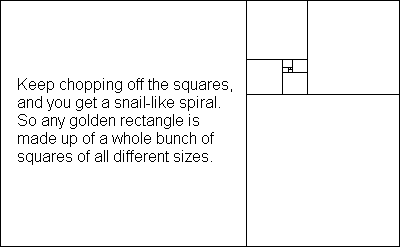
If you stop to think about these squares, you’ll see how they’re related to Fibonacci’s number series. Going outward through the spiral, each square gets “added” to the one before it, just like Fibonacci’s numbers are always the result of adding the previous two numbers.
This pattern is one of the most common in nature. Watch for it.
Insect Intelligence
Fibonacci numbers aren’t the only place where math shows up in plants and animals. One of the most striking uses of math in nature is the six-sided honeycomb pattern used by bees to build their hives. In geometry, we call the shape of a honeycomb a hexagon, because “hex” means six and “gon” means side. (That’s also why any multi-sided structure is called a polygon – “poly” means “many” and therefore polygon means many-sided.)

For a long time, people wondered about honeycombs. Why did they always have 6 sides? And how did the bees know to build them this way?
Then mathematicians discovered that the hexagonal structure used in honeycombs has a very special property: it’s the strongest structure you can build from a limited amount of material. In other words, if you’re trying to build something that’s strong and lightweight, hexagons are the way to go.
This is why many of the walls and other parts on airplanes have a honeycomb-like pattern inside of them. Engineers have designed these parts to be strong but lightweight, and they’re using the same design that bees have used for millions of years. When my father worked at Boeing, he once brought home for me a piece of the material they use to make the sides of airplanes. It was two pieces of sheet metal with a fine honeycomb pattern of paper glued between them. The paper was easy to tear, but I could jump up and down on the honeycomb made from that same paper and it wouldn’t give a bit.
This is a good example of how we can learn from insects and other animals. They’ve been around a lot longer than human beings have been, and they’ve already figured out some of the things that we still need to learn.

Here’s another thing that bees have figured out, but we still don’t understand: how do they fly? Sure, we all know they flap their wings up and down, but there’s a problem: their wings aren’t actually large enough to lift their bodies off the ground, no matter how fast they flap. In fact, there are scientists who can “prove” that bees can’t fly. Bees, not knowing how to read those scientific proofs, just go right on flying because they don’t know that it’s impossible. If we can ever understand how bees do this, it might help us to build better airplanes and helicopters.

The so-called “social insects” also know a lot about working together. These are the insects that live in groups and are usually surrounded by hundreds or thousands of their species. Ant colonies, bee hives, and termite colonies are all good examples of social insects at work.
Scientists that study insects (they’re called entomologists) used to think that there were certain insects “in charge,” and that they somehow told the others what to do. After careful study, however, the scientists couldn’t find any signs that this is actually happening. Instead, it appears that each insect has a role, and it simply performs its role without any consideration of the goals of the colony as a whole. In other words, each insect in a social group just does its job, and there are no insects in charge whose job it is to tell other insects what to do next.
An ant whose role is “grab food and drag it back to the other ants” will usually do so when it finds food, and the rest of the time it appears to be wandering aimlessly. Another ant whose role is “build tunnels” will do that at every opportunity, and may not look twice at a piece of food, since that isn’t its job. Somebody else will bring it back to the anthill, where they can all have a big feast later.
This manner of working together (specialization) is used in large organizations of humans as well, but we’ve only started doing this in the last few thousand years. Insects have used these techniques for millions of years, and – like so many other things – we didn’t figure it out until long after they did.
Moths

When I was a little boy, I noticed that there were always lots of moths around the porch light in the morning if the light had been left on all night. Since I liked to look at the moths and catch them, I would sometimes leave the porch light on just to see what I could catch. The next morning, I would get up early to check what kinds of moths had come to roost on our porch. Opening the door would scare them away, so I would go out the back door and around to the front, sneaking up on them with a glass jar or a butterfly net, hoping to catch a new colorful type of moth that I had never seen before.
When I caught moths like this, I sometimes wondered why they flew toward the porch light at night. In order to understand their thinking, though, I had to learn to see things like a moth. And to see things like a moth, you have to understand how their eyes are different from ours.
Moths have multi-faceted eyes, which means that the eyeballs are each made up of thousands of little lenses. These lenses are hexagonal shaped, like the bee’s honeycombs, because that makes the eyeball very sturdy.
The eyeball itself is locked in place – it doesn't move like our eyes. So each lens is always pointing in the same direction from moth's body. The only way to point a lens at something is for the moth to move its entire body.
When a moth flies, it tries to keep a bright light source locked into one of the lenses, and its entire body moves to keep that lens focused on the light. Insects probably developed this technique millions of years ago, when the only lights they could see were the moon at night and the sun during the day – if you use this technique with the moon or the sun, it’s a good way to fly in a straight line.
But with lights nearby – street lights, Christmas lights, headlights, and other lights – it doesn’t work very well. This is because the moth locks on to a circle around the light source, and travels in that circle. If the light source is millions of miles away, then the circle is so big that the moth travels in nearly a straight line. But if the light source is nearby, then the circle is tight, and the moth spins inward on tighter and tighter loops around the light.
Here’s a fun experiment to see how this works. Go out in a wide-open area and pretend that you’re a moth. Then pick something that we’ll pretend is the light or the flame. It could be a friend standing nearby, or a tree, or anything else. Now point your finger at the make-believe light, and start walking forward.
Keep your finger pointed at the light, and – this is the important part! – don’t let your arm or finger change their angle with your body. Make them immovable, just like a lens in a moth’s eye.
Here’s what will happen: you’ll be locked into a spiral around the light. If the light is nearby, you’ll spiral inward and get to it quickly. If the light is far away, you’ll be going in a pretty straight line, but it’s just a much bigger spiral that will also eventually lead to the light. Now you know what it’s like to be a moth!
Because of this simple flight pattern, all moths are attracted to lights. It’s not that they really want to go to the light, of course. It’s just that their method for flying in a straight line causes them to circle inward toward nearby lights.
In the old days, before man discovered fire, things were simpler for moths. The only points of light at night were the moon and stars, which were very far away. A moth could fly in a relatively straight line by simply keeping any point of light at a fixed angle to the side, and flying on the arc of a circle around that point of light; the curvature of the arc wasn't much of a problem. But in today's brightly lit-up world, with nearby points of light everywhere, moths can't do that.
Want to catch some pretty moths the next time you go camping? It’s easy, if you have three things: a full moon, a clear night, and some molasses. Find a tree standing by itself, out in the open. Then paint the trunk of the tree with molasses. Moths will be attracted to the light reflecting off the trunk, and when they land on it they’ll stay there because they like the sugar in the molasses. And also because their feet get stuck in the molasses, of course. Try it!
